Determine Missing Side Lengths
How to Determine Missing Side Lengths Using the Pythagorean Theorem
One of the most well-known theorems in mathematics is the Pythagorean Theorem, which is particularly important when examining triangles. In order to enable you to confidently approach challenges, this article will walk you through the several applications of the Pythagorean theorem.Determine Missing Side Lengths geometry spot games

The Theorem of Pythagore
A fundamental relationship between the lengths of a right triangle’s three sides is clarified by this theorem. Importantly, only right triangles are covered by the Pythagorean theorem.Determine Missing Side Lengths geometry spot roblox
A right triangle’s salient characteristics include:geometry spot activities geometry spot.ooo
- A right angle is made up of one internal angle that is 90 degrees.geometry spot unblocked geometry spot.us
-
-
- The hypotenuse, or longest side, is always on the other side of the right angle.Determine Missing Side Lengths geometri spot
-
According to the theorem, the hypotenuse’s square length in a right triangle is equal to the sum of the squares of its other two legs:
c² = a² + b²
The hypotenuse is shown here by the letter c, and the other two sides are shown by the letters a and b, which can be used interchangeably. geometry spot us
How a right triangle is identified
Verifying that the triangle in question is a right triangle is essential before using the Pythagorean theorem. The simplest indicator is the existence of a right angle, which is frequently shown by a square symbol. Determine Missing Side Lengths geometry spot ooo

As an alternative, you can identify a right triangle using:
- Perpendicular sides: A right angle is present if two sides are perpendicular, for example, one vertical and the other horizontal. Perpendicularity can also be indicated by directional indicators such as North and East/West.
- The following theorems apply to triangle elements: The existence of a right angle is confirmed by the fundamental characteristics of tangents, for example, if one side is a tangent and the other is a radius.
- Properties of shapes: Since right angles are inherent to shapes like squares and rectangles, it is crucial to take these characteristics into account.Determine Missing Side Lengths
How to Determine Side Lengths That Are Missing
Finding the missing side lengths in a right triangle is the simplest application of the Pythagorean theorem. Let’s examine one such instance:
Example #1:
Determine which side of the following right triangle is missing.Determine Missing Side Lengths
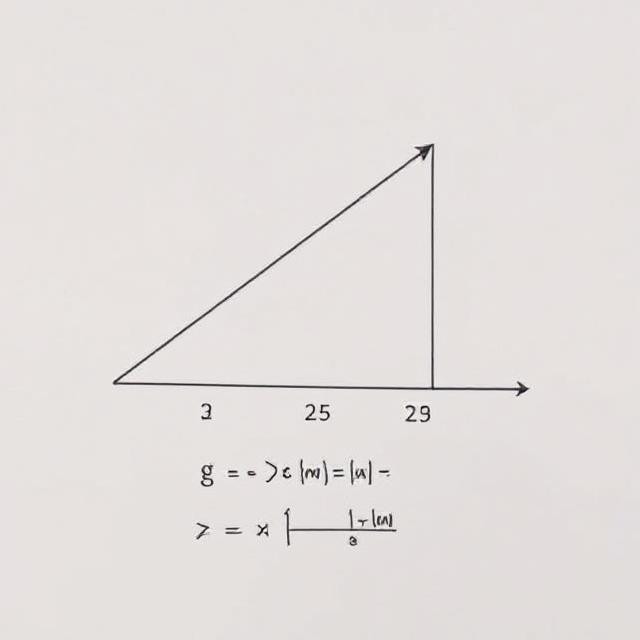
The hypotenuse, or longest side, is the one that lacks length.
Step 1: Write “a,” “b,” and “c” on the sides.Determine Missing Side Lengths
For ease of use when using the Pythagorean theorem, we label the right triangle. The hypotenuse in this case is always “c,” and a and b can be used interchangeably.
Assume b = 12 in and a = 5 in.
Step 2: Enter the Pythagorean Theorem with the known and unknown numbers.
C2 is equal to a2 + b2.
c2 = 52 + 122
Step 3: Make things simpler and figure out c
c2 = 25 + 144
c2 = 169
c = -169
c = 13.
Thus, 13 inches is the missing side length.
Now let’s examine an example with a real-world setting.Determine Missing Side Lengths
Missing Side Length Question in Real Life
Mike is painting a mural on a tall, vertical wall while utilizing a ladder. He places the ladder one and a half meters from the wall’s base. What is the highest wall Mike can reach if the ladder is five meters long?

Step 1: Check the triangle on the right.
The ladder, wall, and floor are the three sides of a right triangle since the angle formed by the vertical wall and the floor is a right angle.
Step 2: Determine which sides
The Pythagorean theorem can be used to determine Mike’s maximum height. According to the theorem, in a right triangle, the square of the hypotenuse’s length—in this example, the ladder—is equal to the sum of the squares of the lengths of the other two sides, which are Mike’s reachable height and the distance between the wall’s base and the ladder.
Utilize the Pythagorean theorem in step three.
C2 is equal to a2 + b2.
Where:
C is the ladder’s length, which is 5 meters.
The distance a between the ladder and the wall’s base is 1.5 meters.
Mike’s maximal height (what we’re looking for) is denoted by b.
Step 4: Replace and figure out b
52 = 1.52 + b2
52 minus 1.52 is b2.
b2 = 25 minus 2.25
b2 equals 22.75
b = -22.75
b = 4.77 (2 d.p.)
Therefore, Mike’s maximum height on the wall is about 4.77 meters.